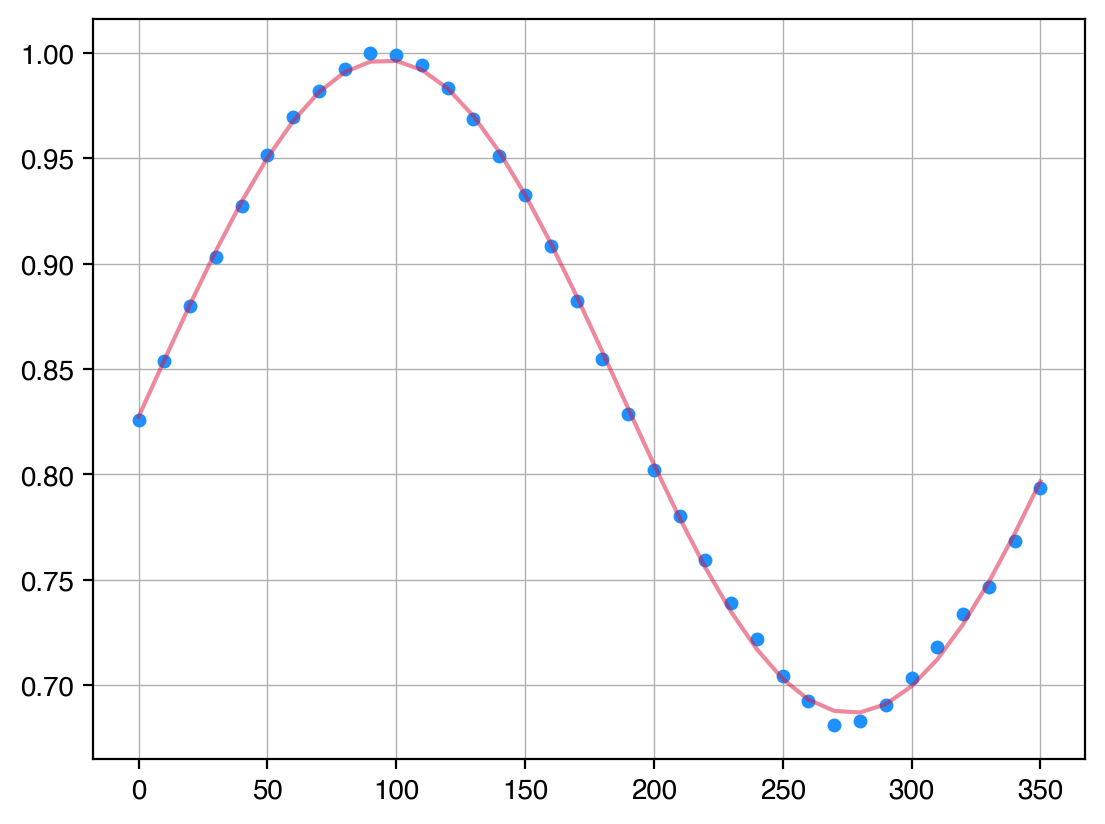
scipy.curve_fitによる三角関数をつかったモデルフィット
1つのファイルで完結する簡単な例。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#!/usr/bin/env python
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt
x = [
0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170,
180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290, 300, 310, 320, 330, 340, 350
]
y = [
0.82588192, 0.85386846, 0.87985536, 0.90294279, 0.92744663, 0.95140891,
0.96978054, 0.98171169, 0.99232641, 1., 0.99891687, 0.99444269,
0.9832864, 0.96853077, 0.95128393, 0.93248738, 0.90825015, 0.88215494,
0.85495159, 0.82853977, 0.80223626, 0.78005699, 0.75953575, 0.73908117,
0.72210095, 0.70438753, 0.69248971, 0.68112513, 0.68318308, 0.69080669,
0.7034627, 0.71821833, 0.73359051, 0.74643815, 0.76822583, 0.7936295
]
def fit_func(x, a, b, c, d):
return a * np.cos(b*(x/360.0*np.pi*2 - c)) + d
popt, pcov = curve_fit(fit_func, x, y, p0=(0.5, 1.0, 100, 0.5))
print(f"best-fit parameters = {popt}")
print(f"covariance = \n{pcov}")
fig, p = plt.subplots(1, 1, sharex=True)
p.plot(x, y, "o", markersize=5, markerfacecolor="dodgerblue", markeredgewidth=0.0, fillstyle="full")
p.plot(x, fit_func(np.array(x), *popt), alpha=0.5, color="crimson")
p.grid(linewidth=0.5)
fig.savefig("fit.png", dpi=200, bbox_inches="tight")
fit.pyとして保存して実行すると、以下のようなフィット結果が表示され、データをベストフィットモデルがfit.pngというファイル名で保存されます。
1
2
3
4
5
6
7
8
9
10
$ python fit.py
best-fit parameters = [-0.15493476 0.99564022 99.4872329 0.8417201 ]
covariance =
[[ 5.86142573e-07 -4.92232088e-07 4.77647902e-05 -1.44058993e-08]
[-4.92232088e-07 6.80976309e-06 -6.60882781e-04 2.05787254e-07]
[ 4.77647902e-05 -6.60882781e-04 6.41615420e-02 -1.99869953e-05]
[-1.44058993e-08 2.05787254e-07 -1.99869953e-05 2.82630860e-07]]
$ open fit.png